I haven’t had much time to work on this for the last month or so because work got a little crazy. Now that the Big Project is over, I’ve started back into this.
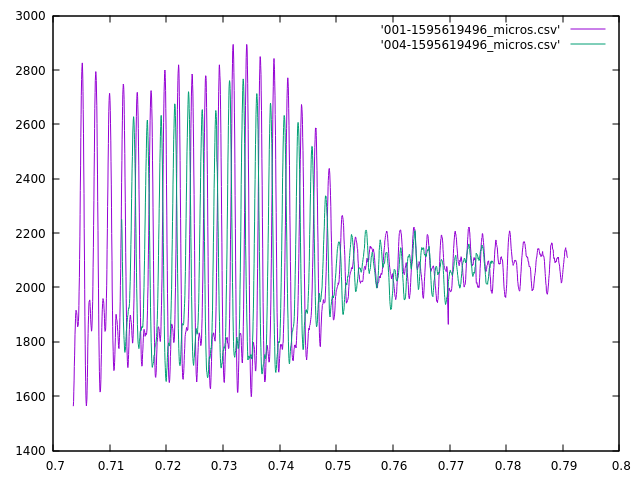
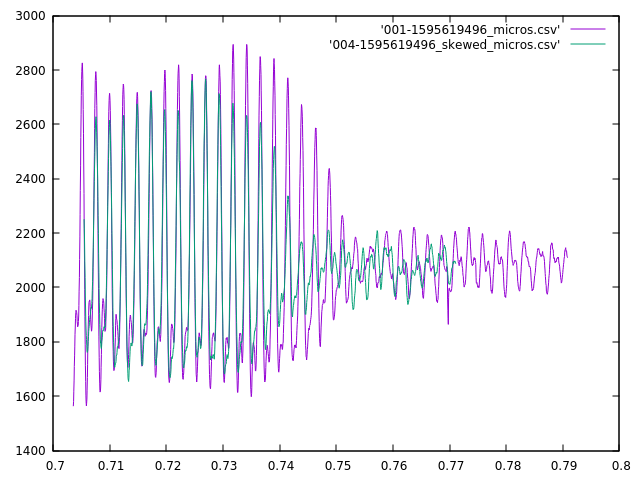
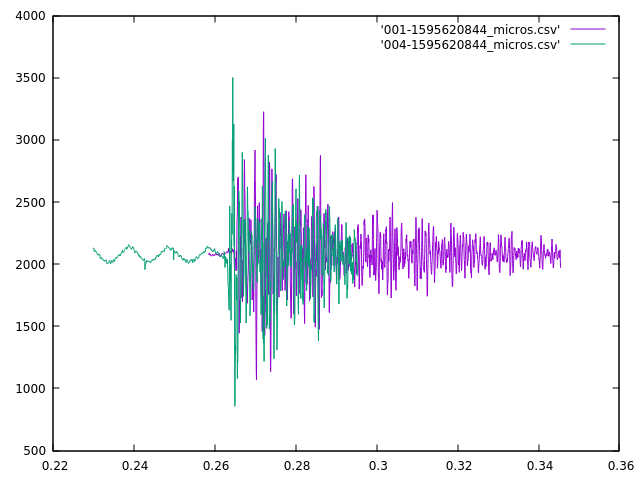
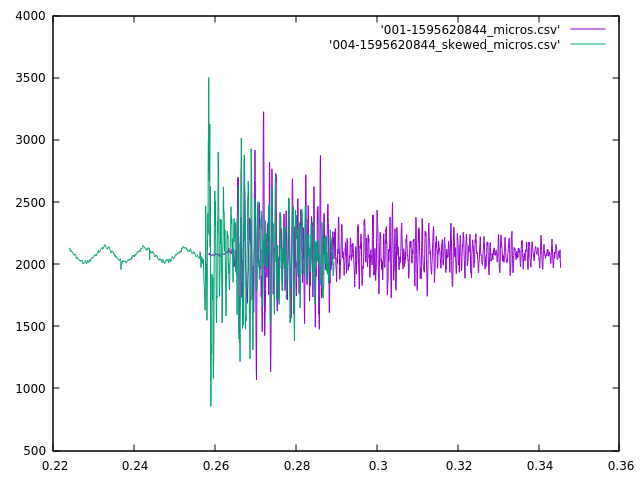
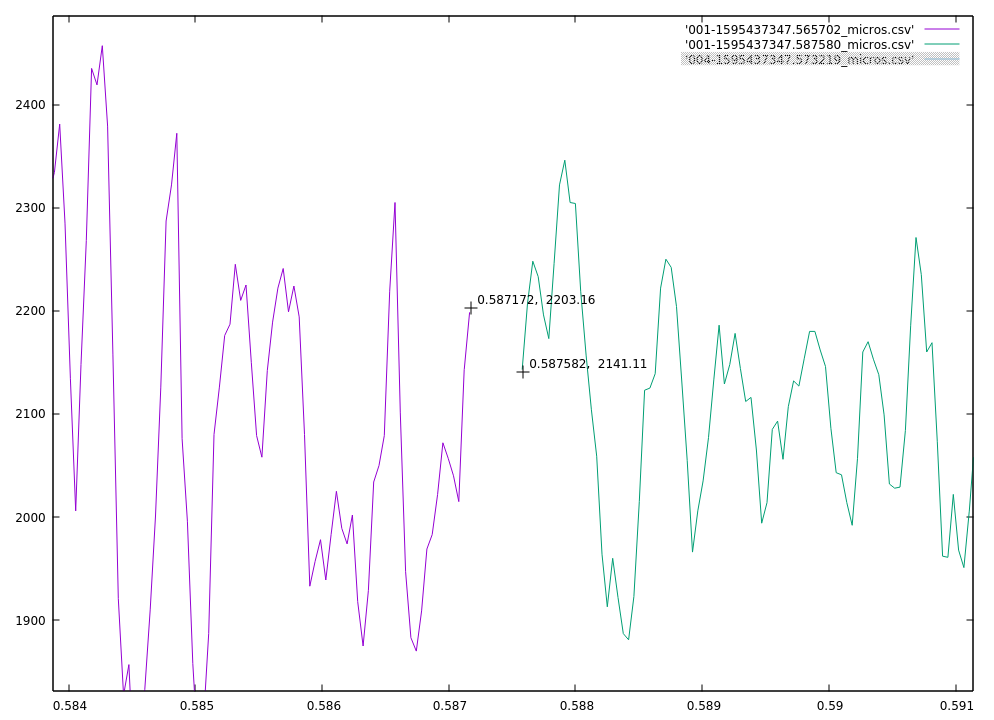
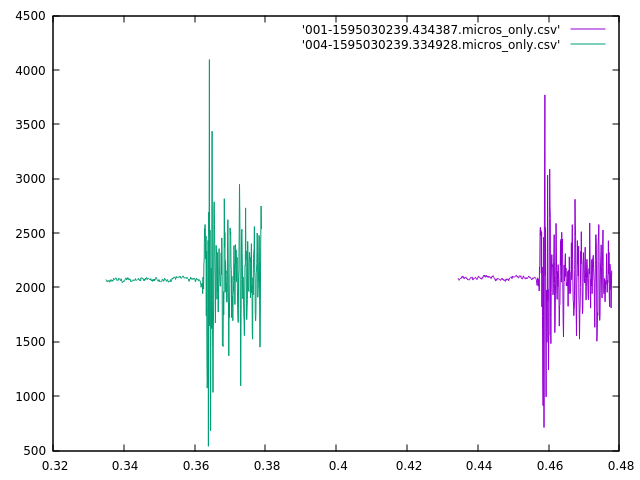
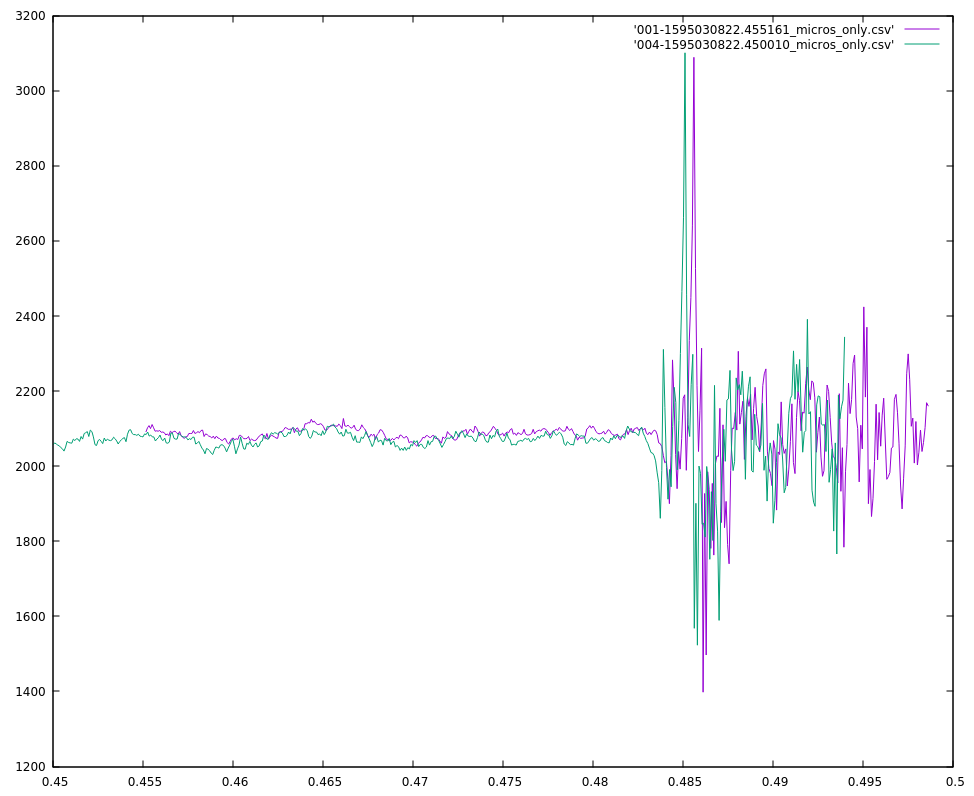
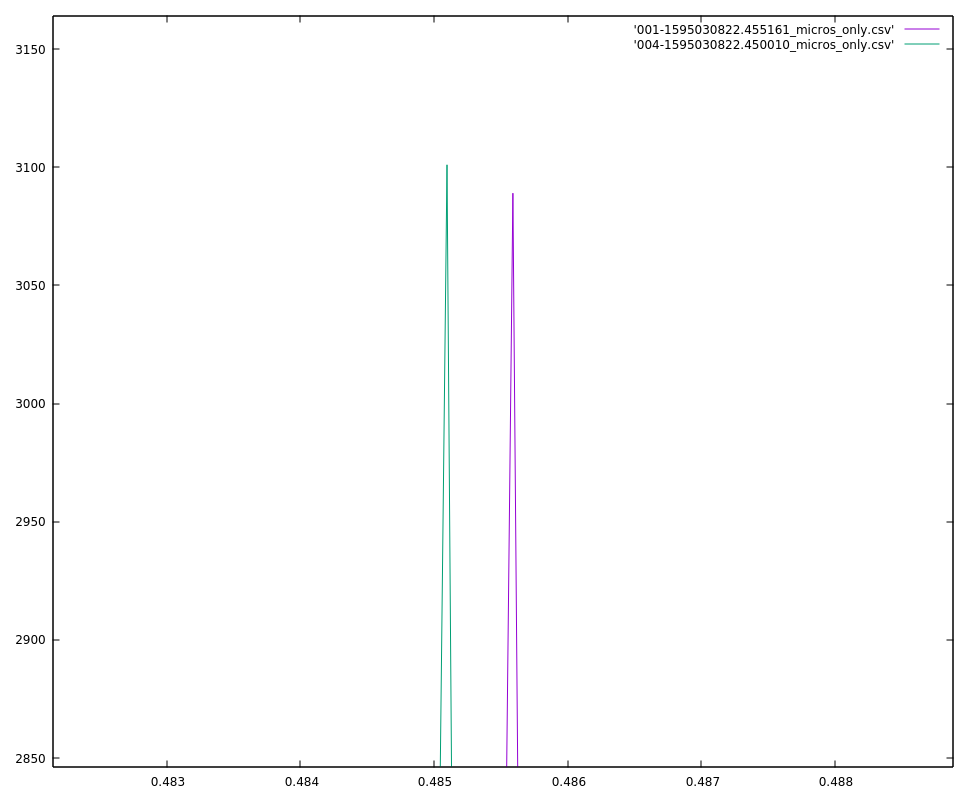
My first attempt at the triangulation is more complex than I initially expected. First I take each sound pair, and using the skew and the locations of the microphone, calculate a pair of bearings originating from the midpoint between those two microphones. Then I take those midpoints and bearings to calculate intersections, and I get four intersections for each pair of midpoints, and there can be up to 6 midpoints, therefore 15 midpoint pairs, and 60 locations. However, I ignore midpoint pairs that are too close together (2 meters or less), and also discard any location more than a couple of kilometers away as being a false signal, but that still leaves between 5 and 25 locations.
Next I try to cluster the locations by finding locations that are within 100m of each other. This isn’t working quite as well as I had hoped, but that is likely due to poor data quality. I’ve just got got the microphones scattered around my office, rather than at the corners of my property, but the algorithm is assuming the mics are at their final location. Because of the relatively low skew times, the calculations are all coming out as if the sounds originate in the center of my house.
I’ve got to work on the enclosures so I can get the microphones to their proper locations. Unfortunately the fireworks that were pretty common near the 4th of July have abated, so I will have relatively few data points to work with.