As I mentioned at the end of the last post, I’ve been assuming that the sound wave was flat, when in fact it is round. now as long as the distance to the source of the sound is much larger than the distance between the two microphones, then this is a pretty good approximation. But what if the source is closer? Consider this:

Now the difference in times is t=(|r2|-|r1|)/v, but we don’t know either r1 or r2, only their difference. We can try to solve for all the places where the difference in the distances is that value. Starting with the point along the line connecting the two, we can find all the points where difference in distances is vt:

I’ll spare you the detailed math, but the solution for possible locations is one branch of a hyperbola:
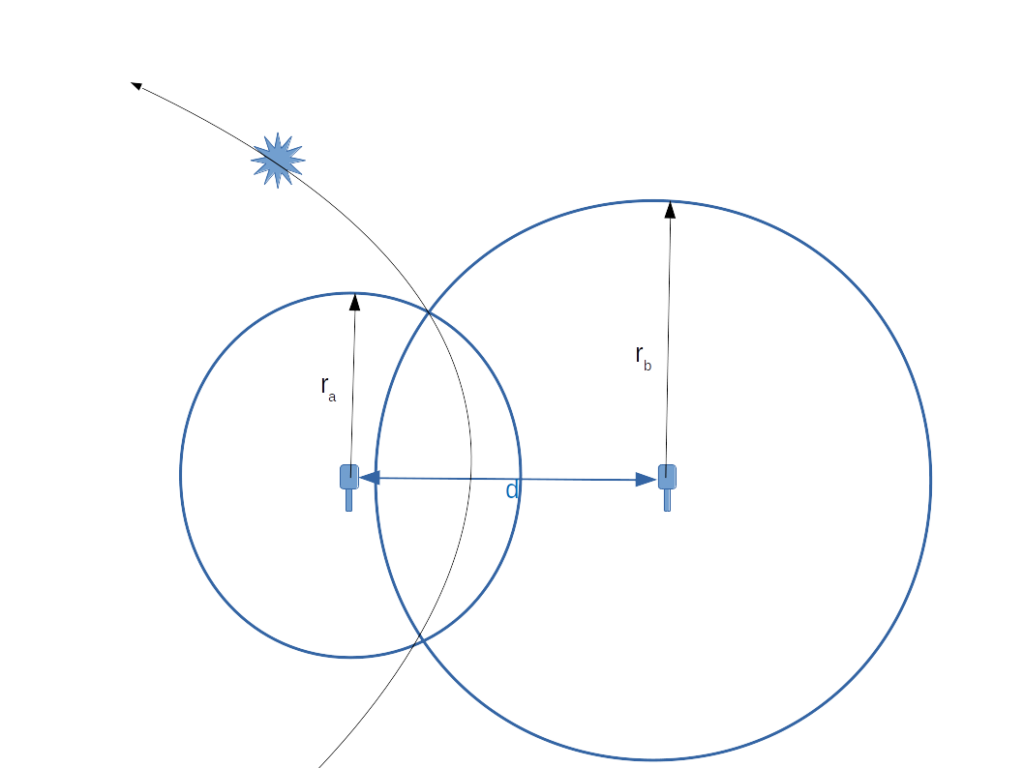
In the limit, you may remember that a hyperbola asymptotically approaches a pair of lines (called asymptotes). These asymptotes are the approximations from my last post. However, with just the measurement from these two microphones, we couldn’t pin down the source any more accurately than somewhere along the hyperbola, but again if we use more than two microphones, we get multiple hyperbolas, and those should only intersect at one point. (hopefully)