The microphones don’t need to be particularly fancy–all I need them to do is identify loud sounds. I’m considering these. Far more critical is identifying when those loud sounds occurred very precisely. Actually, I don’t care about the absolute time, just the relative time each microphone receives the sound.
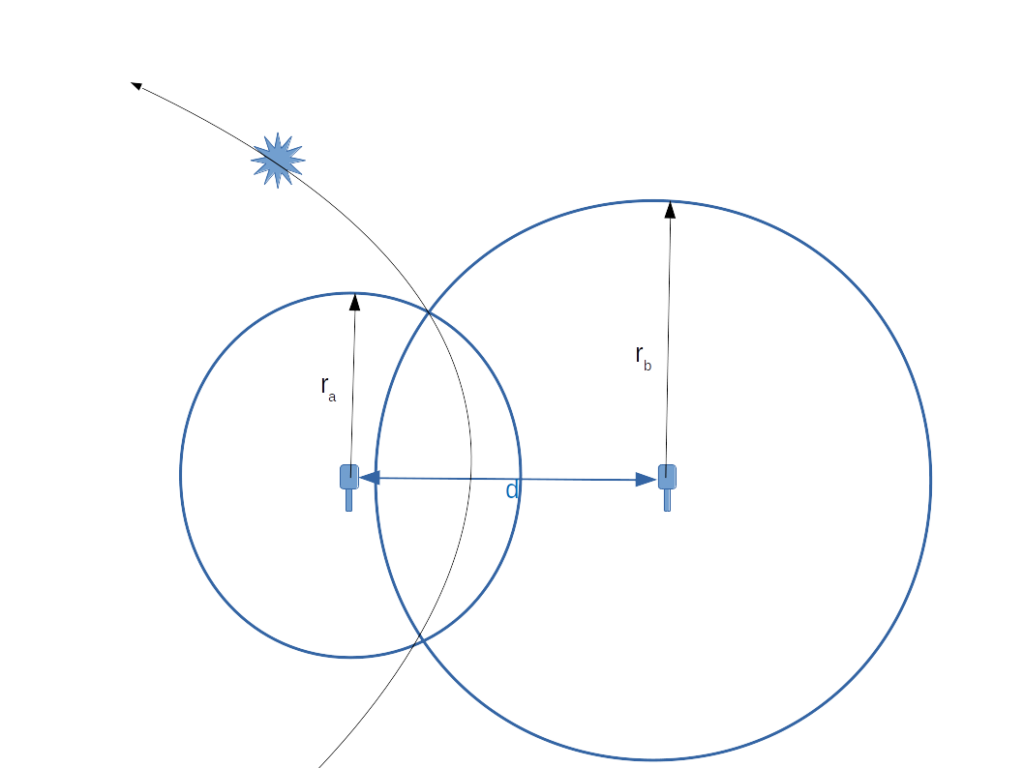
As we saw in the first post, with a baseline of 20 meters (~65 feet)–which is about all I can fit in my back yard, a 1 millisecond difference translates into about a 1 degree difference in direction, and that resolution isn’t good enough to pinpoint something more than a few houses away. I’m shooting for having a resolution of 100 microseconds (and an angular resolution of 1/10th of a degree.) This would require a 10kHz sampling rate, which is about all I can get without going with exotic hardware.
I could use a single computer with an accurate clock to monitor all four microphones directly. This is the simplest solution, but practical limitations on how long you can make the microphone cables and difficulty routing them mean that I’d be limited to relatively short baselines. I may build a simple proof of concept based on this design, but it’s far from ideal.
A more capable solution is to have a small single board computer with each microphone, having them report back to a central host and synchronizing their clocks using WiFi. A linux based computer like a Raspberry Pi or a BeagleBone might work, but the problem is better suited to a dedicated microcontroller with WiFi like the Adafruit Feather HUZZAH–built around a ESP8266 microcontroller, or perhaps an Adafruit Feather M0 WiFi, which has considerably more memory and features, though it’s roughly twice the price–making it nearly as expensive as a Raspberry Pi 3 B. Here’s a table of the trade-offs
| Name | Analog inputs | Clock | WiFi | Battery Management | Total price/mic |
|---|---|---|---|---|---|
| Raspberry Pi 3 B+ | 0 | Y | b/g/n/ac | N | $60 |
| BeagleBone Black | 8 | Y | dongle | N | $80 |
| Feather Huzzah | 1 | N | b/g/n | Y | $30 |
| Feather M0 WiFi | 8 (6 usable) | RTC | b/g/n | Y | $55 |
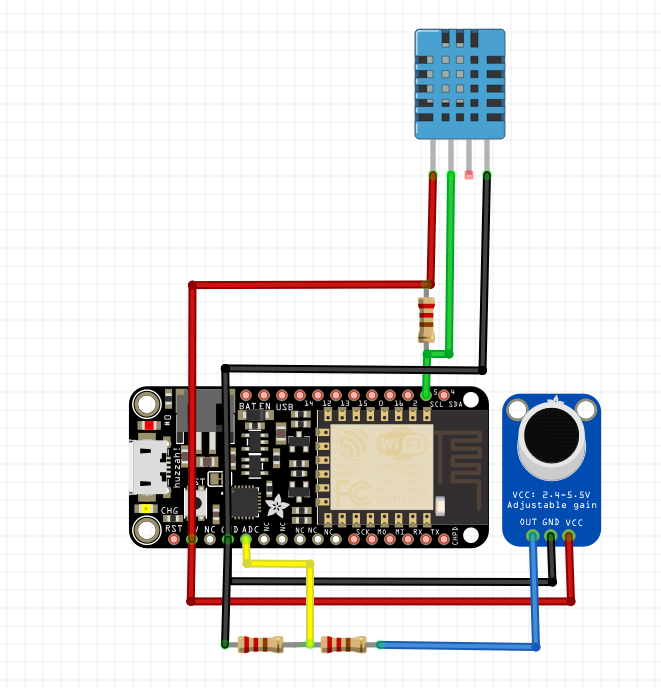
The HUZZAH only has one analog input (with a 1v maximum so I’ll have to use a voltage divider to drop the 3.3v mic output down), and I’m not sure that it has enough memory to handle the WiFi, NTP and the audio code combined. I’ve ordered one to give it a try. Here’s a basic design I came up with (the blue package at the top is a temperature sensor so I can calculate the speed of sound):
The M0 WiFi variant on the other hand, has lots of analog inputs and memory. I’m going to interface it with a RTC (real time clock) chip. The RTC only has a resolution of 1 second for direct measurements, but also provides temperature compensated oscillator which can generate 32kHz, 8kHz, 4kHz, 1kHz and 1Hz square waves, which should allow for some relatively precise measurements. The 8kHz clock would give me a resolution of approximately 125 microseconds, which is pretty close to what I’m looking for. The 32kHz clock could give me a resolution of ~30 microseconds, but the ADC (analog to digital converter) on that cheap chip almost certainly can’t match that rate. The RTC also has the ability to measure temperature. I’ve ordered one of these as well and I’ll do a head-to-head matchup to see which will work better. The relatively hefty price means building 4 M0 boards (with 4 RTCs and 4 microphones) will strain the budget.
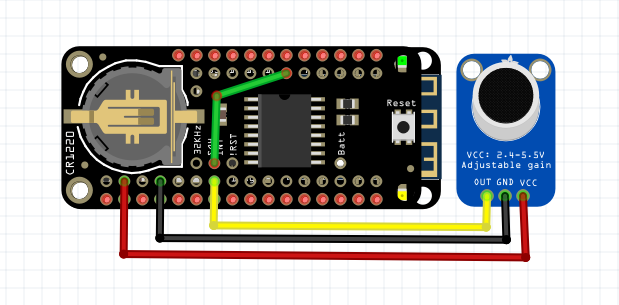
Both of the feather boards have battery management, so I might be able to get away with making them battery/solar powered, meaning even fewer wires to deal with. The range of the WiFi limits the baselines to no more than a hundred to two hundred feet (30-60 meters). For longer baselines I’m considering using the LoRa radio version of the Feather, which might allow for baselines measured in kilometers rather than meters.