After writing up my (computationally intensive) code to measure the skew between the signals from two microphones, I’ve made a discovery. It works great for stuff with complex, low-frequency sounds like my chair creaking, but not so well in other cases. For sustained, constant frequency sounds (like beeps) it gets confused about which of several possible alignments are “best”. Take for example this short beep as heard by two adjacent microphones:
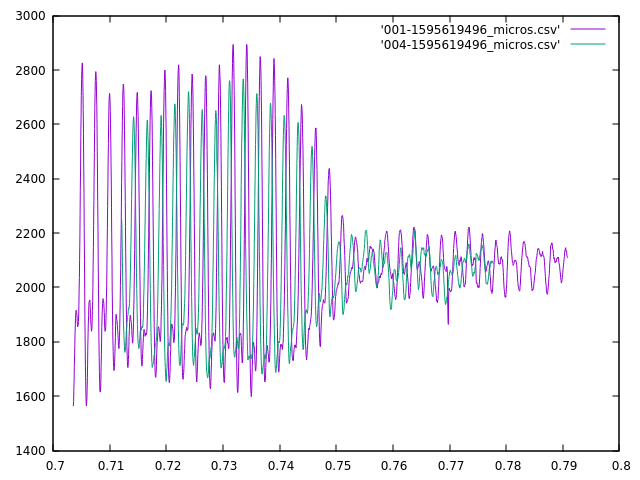
My visual best fit says the green waveform needs to be shifted a few hundred microseconds to the right, and that these were almost in alignment already. However, my algorithm shifted it ~13,000 microseconds to the left.
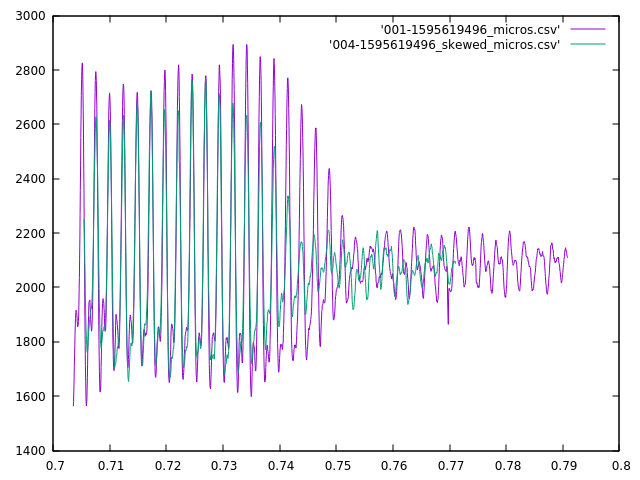
It did make the wave peaks line up, but since this is a more or less steady tone, that happens every couple of milliseconds. I’m also sure it maximized my fit function, but to my eye the overall envelopes don’t match nearly as well. I think there are two factors working against my algorithm here. First, the waveforms weren’t complete–the beginning of the waveforms was cut off by different amounts in the different samples. I’ve taken measures to reduce the likelihood of that happening, but I can’t eliminate it altogether. Second, this was a fairly steady tone–as I already mentioned, and there were lots of “pretty good” fits that it had to choose from.
The other situation that it doesn’t handle well is more problematic. It appears that for short, sharp sounds–like a clap, whip crack, fireworks or gunshots–there is too much high-frequency information that the two mics will sample differently, and since my sampling rate is about 20kHz, I really can only differentiate frequencies below about 10kHz (5kHz for a good fit). See the Nyquist-Shannon theorem for a more complete discussion as to why. So, when I have a signal with a lot of high-frequency information, I can’t really match it effectively. Take this example of a clap when the mics where a few feet apart (1-2 meters):
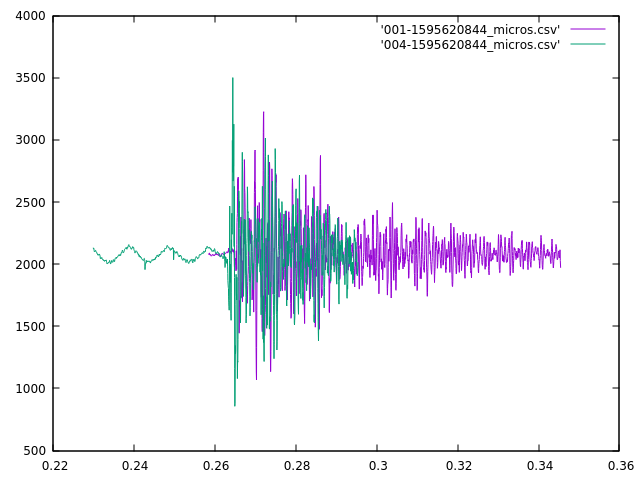
The apparent shift shouldn’t need to be large, but the algorithm doesn’t pay attention to that, and it came up with a fit that looked like:
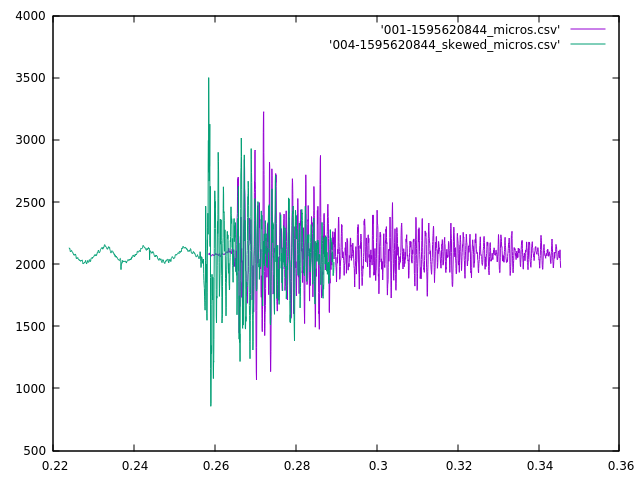
This is a much worse fit according to my eye. I think a better technique in this case it to line up the beginning of the loud sounds, but I need to come up with a way to identify those algorithmically. I’ll probably use some heuristic like looking at the time of the first samples to fall significantly further from the mean than I’d been seeing previously, but that requires that I have a nice quiet section before the sound happens. I’ve taken steps to try to make sure that I have that (by sending the prior buffer as well when I detect an anomaly), but it doesn’t always work out as you can see in the purple curve.